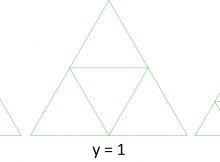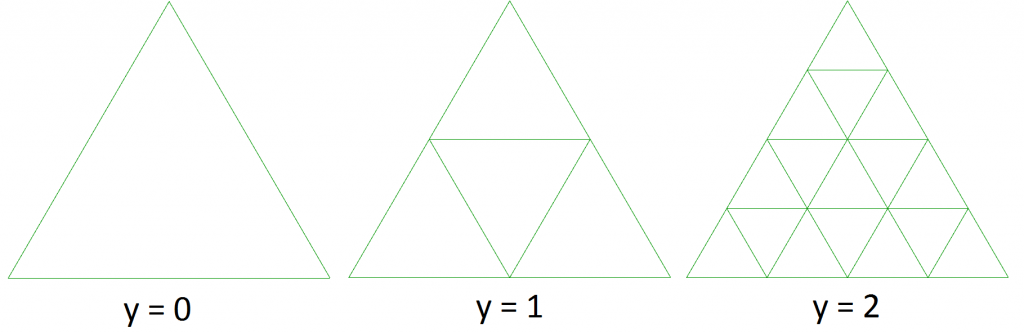A very simple approach to subdividing a mesh in Grasshopper.
What it is
You have a mesh which is made of vertices and mesh faces. Let’s say some of the faces are too large, and you want to divide these large faces into lots of smaller faces.
This script divides all faces into triangles. It them measures the area of each triangle. If the triangle area is above a threshold, it divides that triangle into four smaller triangles.
How to use it
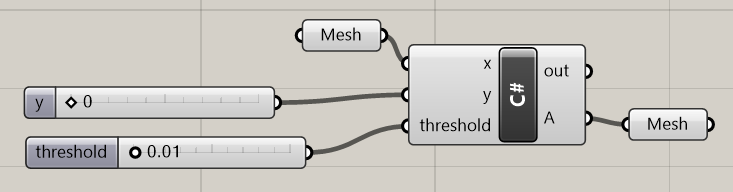
Create a C# component. Set inputs called x, y, and threshold. X is a mesh, Y is an integer, and threshold is a double.
Copy the code below into the C# component.
Feed a mesh into x. Y is the maximum number of subdivisions that will be performed on the mesh. ‘Threshold’ is the area of a ‘big’ mesh face, and the script will try to subdivide any such big faces.
What you get
Here is a slightly more complicated example. Notice how only large faces get subdivided first.
Code
private void RunScript(Mesh x, int y, double threshold, ref object A) { x = Triangulate(x); for (int i = 0; i < y; i++) Subdivide(x, threshold); A = x; } // <Custom additional code> public Mesh Subdivide(Mesh m, double threshold) { List<MeshFace> newFaces = new List<MeshFace>(); foreach (MeshFace mf in m.Faces) { double mfarea = AreaOfTriangle(m, mf); if(mfarea > threshold) { m.Vertices.AddVertices(FaceMidPoints(m, mf)); newFaces.Add(new MeshFace(mf.A, m.Vertices.Count - 3, m.Vertices.Count - 1)); newFaces.Add(new MeshFace(m.Vertices.Count - 3, mf.B, m.Vertices.Count - 2)); newFaces.Add(new MeshFace(m.Vertices.Count - 1, m.Vertices.Count - 2, mf.C)); newFaces.Add(new MeshFace(m.Vertices.Count - 3, m.Vertices.Count - 2, m.Vertices.Count - 1)); } else newFaces.Add(mf); } m.Faces.Clear(); m.Faces.AddFaces(newFaces); newFaces.Clear(); return m; } public List<Point3d> FaceMidPoints(Mesh m, MeshFace mf) { var rtnlist = new List<Point3d>(); rtnlist.Add(MidPoint(m.Vertices[mf.A], m.Vertices[mf.B])); rtnlist.Add(MidPoint(m.Vertices[mf.B], m.Vertices[mf.C])); rtnlist.Add(MidPoint(m.Vertices[mf.C], m.Vertices[mf.A])); return rtnlist; } public Point3d MidPoint(Point3d pt1, Point3d pt2) { return new Point3d(0.5 * (pt1.X + pt2.X), 0.5 * (pt1.Y + pt2.Y), 0.5 * (pt1.Z + pt2.Z)); } public static Mesh Triangulate(Mesh x) { int facecount = x.Faces.Count; for (int i = 0; i < facecount; i++) { var mf = x.Faces[i]; if(mf.IsQuad) { double dist1 = x.Vertices[mf.A].DistanceTo(x.Vertices[mf.C]); double dist2 = x.Vertices[mf.B].DistanceTo(x.Vertices[mf.D]); if (dist1 > dist2) { x.Faces.AddFace(mf.A, mf.B, mf.D); x.Faces.AddFace(mf.B, mf.C, mf.D); } else { x.Faces.AddFace(mf.A, mf.B, mf.C); x.Faces.AddFace(mf.A, mf.C, mf.D); } } } var newfaces = new List<MeshFace>(); foreach (var mf in x.Faces) { if(mf.IsTriangle) newfaces.Add(mf); } x.Faces.Clear(); x.Faces.AddFaces(newfaces); return x; } public double AreaOfTriangle(Point3d pt1, Point3d pt2, Point3d pt3) { double a = pt1.DistanceTo(pt2); double b = pt2.DistanceTo(pt3); double c = pt3.DistanceTo(pt1); double s = (a + b + c) / 2; return Math.Sqrt(s * (s - a) * (s - b) * (s - c)); } public double AreaOfTriangle(Mesh m, MeshFace mf) { return AreaOfTriangle(m.Vertices[mf.A], m.Vertices[mf.B], m.Vertices[mf.C]); }
Caveats
This code is WIP. It is by no means the most efficient or correct way (by a long shot!) of doing this – it merely fulfilled a task I had at the time.
It also returns what Grasshopper reckons is an ‘invalid mesh’. I suspect that this is because vertices are generated that overlap other faces without also being one of their vertices, but I’m not quite sure. Despite this warning, it does still produce a usable mesh.
Further reading
I have written about the mesh data structure here, which is probably helpful if you want to understand what’s happening in the above code.
The algorithm for calculating the area of a triangle comes from Heron’s Formula.
I have also published some C# code for triangulating a mesh here.