polyline Archives - James Ramsden

Get points from polyline in RhinoCommon/Grasshopper C# component

Polylines are highly lightweight forms of curves that have many useful applications in Rhino and Grasshopper.

What is a polyline?

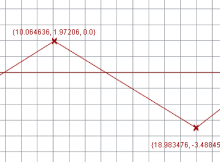
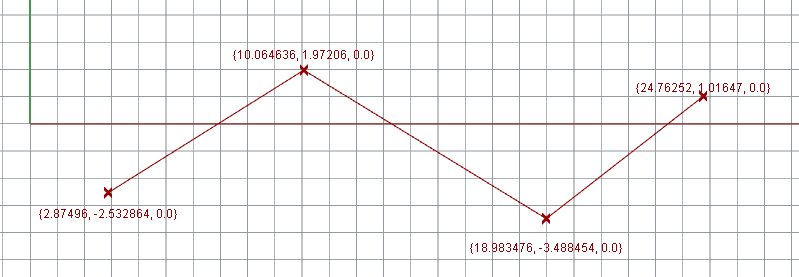
A polyline is a list of points, nothing more. When Rhino reads in a polyline, it creates the curve by doing a dot-to-dot of the points.

It can also be thought of as an interpolation of points with degree = 1. The curve will always pass through the inputted points.

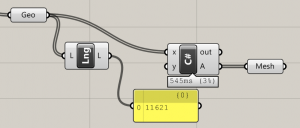
Extracting the points from a polyline

Let’s say you have a polyline as input in Grasshopper. You want to extract the list of points used to create that polyline within a C# script.

The most intuitive method is to look for a property of the polyline called ‘Points’ or something like that. But if we try and find it…

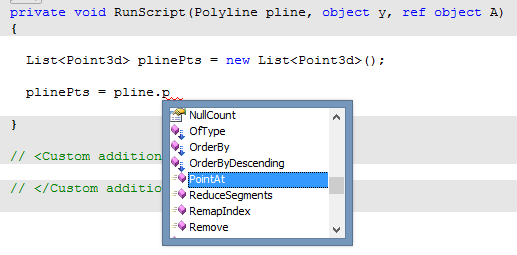
…there’s nothing there! So if there’s no property containing the points, where is this data?

Method 1: Get the whole list of points

As shown in the RhinoCommon SDK documentation, PolyLine inherits from the Point3dList, which itself inherits from the RhinoList class.

We can use the ToList() method to get the list of points:

  private void RunScript(Polyline pline, object y, ref object A)
  {
    var pts = new List<Point3d>();

    pts = pline.ToList();

    A = pts;
  }

Method 2: Get a single point

We can extract a single point from the ToList() method:

  private void RunScript(Polyline pline, object y, ref object A)
  {
    var pt = new Point3d();

    pt = pline.ToList()[0];

    A = pt;
  }

Or, even shorter, we can treat the polyline like a list itself and access the points directly:

  private void RunScript(Polyline pline, object y, ref object A)
  {
    var pt = new Point3d();

    pt = pline[0];

    A = pt;
  }

Thanks to Fraser Greenroyd for our joint effort in unpicking this deceptively unintuitive challenge – he also wrote about it here.

Check whether points are inside a polyline curve in Grasshopper with C#

Let’s say you have a polyline in Grasshopper. You also have some points, some of them inside the curve and some of them outside. You want to sort the points depending on whether they are inside or outside the curve.

This component allows you to do that. Input your polyline and your points to check. The ‘A’ list will contain the points inside the curve, and the ‘B’ list will contain the points outside the curve.

This will then produce the following output:

Download component

The following component is a user object that allows the input of a single polyline.

Points inside curve (Grasshopper user object component)

1 file(s) 2.52 KB

Download

If you are working with multiple polylines, and want to check that points are inside or outside every polyline at once, have a look at this file instead.

Source code

If you prefer, you can use the source code directly from below. It is formatted for the C# component in Grasshopper, though of course it can be easily generalised.

private void RunScript(List<Point3d> pts, Polyline crv, ref object A, ref object B)
  {

    var inside = new List<Point3d>();
    var outside = new List<Point3d>();

    foreach (Point3d pt in pts)
    {
      if(IsInside(pt, crv))
      {
        inside.Add(pt);
      }
      else outside.Add(pt);
    }
    A = inside;
    B = outside;

  }

  // <Custom additional code> 

  bool IsInside (Point3d pt, Polyline crv)
  {
    Point3d pt1, pt2;
    bool oddNodes = false;

    for (int i = 0; i < crv.SegmentCount; i++) //for each contour line
    {

      pt1 = crv.SegmentAt(i).From; //get start and end pt
      pt2 = crv.SegmentAt(i).To;

      if ( (pt1[1] < pt[1] && pt2[1] >= pt[1] || pt2[1] < pt[1] && pt1[1] >= pt[1]) && (pt1[0] <= pt[0] || pt2[0] <= pt[0]) ) //if pt is between pts in y, and either of pts is before pt in x
        oddNodes ^= ( pt2[0] + (pt[1] - pt2[1]) * (pt1[0] - pt2[0]) / (pt1[1] - pt2[1]) < pt[0] ); //^= is xor
      //end.X + (pt-end).Y   * (start-end).X  /(start-end).Y   <   pt.X
    }


    if (!oddNodes)
    {
      double minDist = 1e10;
      for (int i = 0; i < crv.SegmentCount; i++) {
        Point3d cp = crv.SegmentAt(i).ClosestPoint(pt, true);
        //Point3d cp = mvContour[i].closestPoint(pt);
        //minDist = min(minDist, cp.distance(pt));
        minDist = Math.Min(minDist, cp.DistanceTo(pt));
      }
      if (minDist < 1e-10)
        return true;
    }

    if(oddNodes) return true;

    return false;
  }

FastMesh v2: The stupidly easy way of creating efficient meshes from polylines

In a recent post, I found that converting polylines to meshes in Grasshopper can be problematic. Using a patch to create a mesh from a curve is slow, and directly converting from a curve to a mesh resulted in an inefficent mesh with too many faces.

It seemed that in Grasshopper, there was no easy way to create efficient meshes from closed polylines, so I set about creating my own component. It produced meshes like this:

But in cases with more complicated geometry, it didn’t always work – in the details, it would sometimes miss out triangles, or the mesh edge didn’t quite line up with the original boundary.

Revisiting the problem today, my colleague David Greenwood pointed me towards a method he’d found within the Rhino API – and we can access it in both the C# component and through visual studio. This method produces a mesh from a closed polyline – but amazingly, it returns the kind of efficient mesh we were wanting all along. And as a bonus, it’s really fast too!

The command you need is very simple:

A = Rhino.Geometry.Mesh.CreateFromClosedPolyline(pline);

We tried this method to create the roof tops of a whole city centre, with over 11000 building outlines as polylines. This is the result:

Click the image above for full size.

Zooming in on an image, we can see that, bearing in mind that mesh faces like to be in triangles, the meshes seem to be roughly as efficient as we could imagine:

And how long did these 11000 meshes take to generate? About half a second!

And if, instead of using the C# component, we write the code into a compiled component, such as when we create components with Visual Studio, the time is less than 300ms.

And if that is still too slow, we could also parallelise it, potentially bringing that time under 100ms.

So much for ripping out my hair trying to write my own algorithm or dig around for one elsewhere – I needn’t have bothered because it’s already implemented in Rhino!