Tag: C#

Some pointless fun with C# and the Grasshopper timer

I made a thing, and it ripples!

It could be sound in an auditorium. It could be waves in water. It could be energy dissipating from an earthquake’s epicentre. But that’s not the point.

What it is is a great demonstration on what you can make with the Grasshopper timer, and bit of C#, and 15 minutes to kill.

In the C# component, there are two regions you can edit: the RunScript section, and the ‘additional code’ section. Data stored in RunScript is volatile – it gets deleted every time the component is run. But data stored in the second region is preserved.

By running a timer on our component, it will be executed repeatedly. We can use this second region to hold information between these executions, allowing us to build up complex and dynamic behaviour in Grasshopper.

Grasshopper component C# timer example

The code within the C# component handles each ‘frame’ of the animation. It maintains the current time (increasing by 1 for each cycle) and uses this time to decide what colour each part of the mesh will be.

  private void RunScript(bool _clap, bool _reset, Mesh _mesh, ref object A)
  {
    
    thetime++;

    //button actions
    if(_clap)
    {
      times.Add(thetime);
    }
    if(_reset)
    {
      times.Clear();
      thetime = 0;
      CalcDistances(_mesh, new Point3d(0, 0, 0));
    }

    //maintain list size to maintain performance
    if(times.Count > 50) times.RemoveAt(0);

    //calculate mesh colours
    _mesh.VertexColors.Clear();
    int i = 0;
    foreach(var v in _mesh.Vertices)
    {
      bool shouldbegreen = false;
      foreach(var time in times)
      {
        if(thetime == (time + (int) (distances[i])))
        {
          shouldbegreen = true;
        }
      }
      if(shouldbegreen)
      {
        _mesh.VertexColors.Add(Color.Green);
        _mesh.Vertices.SetVertex(i, _mesh.Vertices[i].X, _mesh.Vertices[i].Y, 1);
      }
      else
      {
        _mesh.VertexColors.Add(Color.Red);
        _mesh.Vertices.SetVertex(i, _mesh.Vertices[i].X, _mesh.Vertices[i].Y, 0);
      }
      i++;
    }

    //output
    A = _mesh;
  }

  // <Custom additional code> 

  int thetime = 0;
  List<int> times = new List<int>();
  List<double> distances = new List<double>();
  
  //preprocessed here to speed up calculation
  public void CalcDistances(Mesh msh, Point3d pt)
  {
    distances.Clear();
    foreach (var v in msh.Vertices)
    {
      distances.Add(pt.DistanceTo(v));
    }
  }

Create a list of random numbers in C#

Generating random numbers in C# isn’t the most intuitive process. I originally learnt to code back in the day using VB, where generating a random number was as simple as calling the Rnd() function.

In C#, there is slightly more work to do. We first have to create an instance of the Random class, which is non-static. Only then can we call a function to generate a random number for us.

The example below is written for the C# component in Grasshopper, but the gist of it can be used for any C# application.

C# code

  private void RunScript(ref object A)
  {

    var rand = new Random();
    var rtnlist = new List<double>();

    for (int i = 0; i < 100000; i++)
    {
      rtnlist.Add(rand.Next(1000));
    }
    A = rtnlist;

  }

What’s happening here?

We create an instantiation of the Random class. We call this ‘rand’. This is what contains the logic to generate our random numbers.

Since computers are inherently quite terrible at generating truly random numbers, programming languages tend to use pre-programmed lists of random numbers instead. The random class picks a place in the list to start from. Then, every time we call for a new random number, it is simply reading the next value in the list.

This is why the function to generate a new random number is called ‘Next’ – it is simply looking at the next value in its list of random numbers. The 1000 in the brackets specifies that the number returned will be scaled between 0 and 1000. (If we left the brackets blank, the random number would be between 0 and the highest possible integer.)

The script creates a list of 100000 random numbers between 0 and 1000. The output is sent to the variable ‘A’. This is a Grasshopper specific thing – if you were writing this as a method, you could change this to ‘return rtnlist’.

If you need many random numbers, you should still only create one instance of Random, and then use ‘Next()’ to build your collection of random numbers. If you don’t do this, and instead create an instance of ‘Random’ for every random number you need, the resulting numbers may not be random at all.

UTCI: Calculation and C# code

Calculate the UTCI (Universal Thermal Climate Index) in any C# / .NET program.

What is the UTCI?

The UTCI calculates an equivalent perceived temperature based upon air temperature, radiative temperature, humidity and air movement. You may be familiar with the UTCI from weather forecasts when they say something like “the air temperature is 30C but it is going to feel more like 35C”. The UTCI is suitable as a method for calculating outdoor thermal comfort levels.

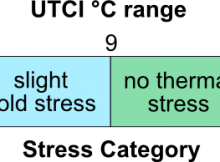
The Equivalent Temperature outputted by UTCI calculations can then be aligned to levels of thermal comfort:

UTCI_scale

Image source

Calculate the UTCI

The interaction between these four values into a single Equivalent Temperature is complex. A function, created via the method of curve-fitting, has been created by Broede as Fortran here, which is a (long!) one-line approximation of UTCI calculation. Fortran isn’t perhaps the most useful language to the average developer today, so what I have done is translate it into C# and tidy it a little by splitting up some methods.

This algorithm has been used in the outdoor comfort component in Ladybug for Grasshopper, where the Fortran code was translated into Python. An online calculator based upon this function is also available here. The source Fortran code is available here.

To use the code below, create a new class in your .NET project and copy the code below. Methods are saved as public static classes.

Example usage

Once you have added the UTCI class in your project (below), you can calculate the UTCI by calling the following method:

double utci = CalcUTCI(temp, wind, mrt, hum);

where:

  • temp: air temperature (degC)
  • wind: wind speed (m/s)
  • mrt: mean radiant temperature (degC)
  • hum: humidity ratio (0-100)

The method returns a double corresponding to the UTCI in degrees C.

Limitations

The approximation function is only valid under the following constraints:

  • Air speed must be betwee 0.5 and 17m/s
  • MRT must be no less than 30C and no more than 70C of the air temperature
  • Air temperature must be between -50C and +50C

UTCI class

    public static class C_UTCI
    {
        /*
         
             !~ UTCI, Version a 0.002, October 2009
    !~ Copyright (C) 2009  Peter Broede
    
    !~ Program for calculating UTCI Temperature (UTCI)
    !~ released for public use after termination of COST Action 730
    
    !~ replaces Version a 0.001, from September 2009

         
         * */
        /// <summary>
        /// Calculate UTCI
        /// </summary>
        /// <param name="Ta">Dry bulb air temp, degC</param>
        /// <param name="va">Air movement, m/s</param>
        /// <param name="Tmrt">Radiant temperature</param>
        /// <param name="RH">Relative humidity, 0-100%</param>
        /// <returns>UTCI 'perceived' temperature, degC. Returns double.min if input is out of range for model</returns>
        public static double CalcUTCI(double Ta, double va, double Tmrt, double RH)
        {

            if (CheckIfInputsValid(Ta, va, Tmrt, RH) != InputsChecks.Pass) return double.MinValue;
            
            double ehPa = es(Ta) * (RH / 100.0);
            double D_Tmrt = Tmrt - Ta;
            double Pa = ehPa / 10.0;//  convert vapour pressure to kPa

            #region whoa_mamma
            double UTCI_approx = Ta +
              (0.607562052) +
              (-0.0227712343) * Ta +
              (8.06470249 * Math.Pow(10, (-4))) * Ta * Ta +
              (-1.54271372 * Math.Pow(10, (-4))) * Ta * Ta * Ta +
              (-3.24651735 * Math.Pow(10, (-6))) * Ta * Ta * Ta * Ta +
              (7.32602852 * Math.Pow(10, (-8))) * Ta * Ta * Ta * Ta * Ta +
              (1.35959073 * Math.Pow(10, (-9))) * Ta * Ta * Ta * Ta * Ta * Ta +
              (-2.25836520) * va +
              (0.0880326035) * Ta * va +
              (0.00216844454) * Ta * Ta * va +
              (-1.53347087 * Math.Pow(10, (-5))) * Ta * Ta * Ta * va +
              (-5.72983704 * Math.Pow(10, (-7))) * Ta * Ta * Ta * Ta * va +
              (-2.55090145 * Math.Pow(10, (-9))) * Ta * Ta * Ta * Ta * Ta * va +
              (-0.751269505) * va * va +
              (-0.00408350271) * Ta * va * va +
              (-5.21670675 * Math.Pow(10, (-5))) * Ta * Ta * va * va +
              (1.94544667 * Math.Pow(10, (-6))) * Ta * Ta * Ta * va * va +
              (1.14099531 * Math.Pow(10, (-8))) * Ta * Ta * Ta * Ta * va * va +
              (0.158137256) * va * va * va +
              (-6.57263143 * Math.Pow(10, (-5))) * Ta * va * va * va +
              (2.22697524 * Math.Pow(10, (-7))) * Ta * Ta * va * va * va +
              (-4.16117031 * Math.Pow(10, (-8))) * Ta * Ta * Ta * va * va * va +
              (-0.0127762753) * va * va * va * va +
              (9.66891875 * Math.Pow(10, (-6))) * Ta * va * va * va * va +
              (2.52785852 * Math.Pow(10, (-9))) * Ta * Ta * va * va * va * va +
              (4.56306672 * Math.Pow(10, (-4))) * va * va * va * va * va +
              (-1.74202546 * Math.Pow(10, (-7))) * Ta * va * va * va * va * va +
              (-5.91491269 * Math.Pow(10, (-6))) * va * va * va * va * va * va +
              (0.398374029) * D_Tmrt +
              (1.83945314 * Math.Pow(10, (-4))) * Ta * D_Tmrt +
              (-1.73754510 * Math.Pow(10, (-4))) * Ta * Ta * D_Tmrt +
              (-7.60781159 * Math.Pow(10, (-7))) * Ta * Ta * Ta * D_Tmrt +
              (3.77830287 * Math.Pow(10, (-8))) * Ta * Ta * Ta * Ta * D_Tmrt +
              (5.43079673 * Math.Pow(10, (-10))) * Ta * Ta * Ta * Ta * Ta * D_Tmrt +
              (-0.0200518269) * va * D_Tmrt +
              (8.92859837 * Math.Pow(10, (-4))) * Ta * va * D_Tmrt +
              (3.45433048 * Math.Pow(10, (-6))) * Ta * Ta * va * D_Tmrt +
              (-3.77925774 * Math.Pow(10, (-7))) * Ta * Ta * Ta * va * D_Tmrt +
              (-1.69699377 * Math.Pow(10, (-9))) * Ta * Ta * Ta * Ta * va * D_Tmrt +
              (1.69992415 * Math.Pow(10, (-4))) * va * va * D_Tmrt +
              (-4.99204314 * Math.Pow(10, (-5))) * Ta * va * va * D_Tmrt +
              (2.47417178 * Math.Pow(10, (-7))) * Ta * Ta * va * va * D_Tmrt +
              (1.07596466 * Math.Pow(10, (-8))) * Ta * Ta * Ta * va * va * D_Tmrt +
              (8.49242932 * Math.Pow(10, (-5))) * va * va * va * D_Tmrt +
              (1.35191328 * Math.Pow(10, (-6))) * Ta * va * va * va * D_Tmrt +
              (-6.21531254 * Math.Pow(10, (-9))) * Ta * Ta * va * va * va * D_Tmrt +
              (-4.99410301 * Math.Pow(10, (-6))) * va * va * va * va * D_Tmrt +
              (-1.89489258 * Math.Pow(10, (-8))) * Ta * va * va * va * va * D_Tmrt +
              (8.15300114 * Math.Pow(10, (-8))) * va * va * va * va * va * D_Tmrt +
              (7.55043090 * Math.Pow(10, (-4))) * D_Tmrt * D_Tmrt +
              (-5.65095215 * Math.Pow(10, (-5))) * Ta * D_Tmrt * D_Tmrt +
              (-4.52166564 * Math.Pow(10, (-7))) * Ta * Ta * D_Tmrt * D_Tmrt +
              (2.46688878 * Math.Pow(10, (-8))) * Ta * Ta * Ta * D_Tmrt * D_Tmrt +
              (2.42674348 * Math.Pow(10, (-10))) * Ta * Ta * Ta * Ta * D_Tmrt * D_Tmrt +
              (1.54547250 * Math.Pow(10, (-4))) * va * D_Tmrt * D_Tmrt +
              (5.24110970 * Math.Pow(10, (-6))) * Ta * va * D_Tmrt * D_Tmrt +
              (-8.75874982 * Math.Pow(10, (-8))) * Ta * Ta * va * D_Tmrt * D_Tmrt +
              (-1.50743064 * Math.Pow(10, (-9))) * Ta * Ta * Ta * va * D_Tmrt * D_Tmrt +
              (-1.56236307 * Math.Pow(10, (-5))) * va * va * D_Tmrt * D_Tmrt +
              (-1.33895614 * Math.Pow(10, (-7))) * Ta * va * va * D_Tmrt * D_Tmrt +
              (2.49709824 * Math.Pow(10, (-9))) * Ta * Ta * va * va * D_Tmrt * D_Tmrt +
              (6.51711721 * Math.Pow(10, (-7))) * va * va * va * D_Tmrt * D_Tmrt +
              (1.94960053 * Math.Pow(10, (-9))) * Ta * va * va * va * D_Tmrt * D_Tmrt +
              (-1.00361113 * Math.Pow(10, (-8))) * va * va * va * va * D_Tmrt * D_Tmrt +
              (-1.21206673 * Math.Pow(10, (-5))) * D_Tmrt * D_Tmrt * D_Tmrt +
              (-2.18203660 * Math.Pow(10, (-7))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt +
              (7.51269482 * Math.Pow(10, (-9))) * Ta * Ta * D_Tmrt * D_Tmrt * D_Tmrt +
              (9.79063848 * Math.Pow(10, (-11))) * Ta * Ta * Ta * D_Tmrt * D_Tmrt * D_Tmrt +
              (1.25006734 * Math.Pow(10, (-6))) * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (-1.81584736 * Math.Pow(10, (-9))) * Ta * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (-3.52197671 * Math.Pow(10, (-10))) * Ta * Ta * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (-3.36514630 * Math.Pow(10, (-8))) * va * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (1.35908359 * Math.Pow(10, (-10))) * Ta * va * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (4.17032620 * Math.Pow(10, (-10))) * va * va * va * D_Tmrt * D_Tmrt * D_Tmrt +
              (-1.30369025 * Math.Pow(10, (-9))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (4.13908461 * Math.Pow(10, (-10))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (9.22652254 * Math.Pow(10, (-12))) * Ta * Ta * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (-5.08220384 * Math.Pow(10, (-9))) * va * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (-2.24730961 * Math.Pow(10, (-11))) * Ta * va * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (1.17139133 * Math.Pow(10, (-10))) * va * va * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (6.62154879 * Math.Pow(10, (-10))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (4.03863260 * Math.Pow(10, (-13))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (1.95087203 * Math.Pow(10, (-12))) * va * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (-4.73602469 * Math.Pow(10, (-12))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt +
              (5.12733497) * Pa +
              (-0.312788561) * Ta * Pa +
              (-0.0196701861) * Ta * Ta * Pa +
              (9.99690870 * Math.Pow(10, (-4))) * Ta * Ta * Ta * Pa +
              (9.51738512 * Math.Pow(10, (-6))) * Ta * Ta * Ta * Ta * Pa +
              (-4.66426341 * Math.Pow(10, (-7))) * Ta * Ta * Ta * Ta * Ta * Pa +
              (0.548050612) * va * Pa +
              (-0.00330552823) * Ta * va * Pa +
              (-0.00164119440) * Ta * Ta * va * Pa +
              (-5.16670694 * Math.Pow(10, (-6))) * Ta * Ta * Ta * va * Pa +
              (9.52692432 * Math.Pow(10, (-7))) * Ta * Ta * Ta * Ta * va * Pa +
              (-0.0429223622) * va * va * Pa +
              (0.00500845667) * Ta * va * va * Pa +
              (1.00601257 * Math.Pow(10, (-6))) * Ta * Ta * va * va * Pa +
              (-1.81748644 * Math.Pow(10, (-6))) * Ta * Ta * Ta * va * va * Pa +
              (-1.25813502 * Math.Pow(10, (-3))) * va * va * va * Pa +
              (-1.79330391 * Math.Pow(10, (-4))) * Ta * va * va * va * Pa +
              (2.34994441 * Math.Pow(10, (-6))) * Ta * Ta * va * va * va * Pa +
              (1.29735808 * Math.Pow(10, (-4))) * va * va * va * va * Pa +
              (1.29064870 * Math.Pow(10, (-6))) * Ta * va * va * va * va * Pa +
              (-2.28558686 * Math.Pow(10, (-6))) * va * va * va * va * va * Pa +
              (-0.0369476348) * D_Tmrt * Pa +
              (0.00162325322) * Ta * D_Tmrt * Pa +
              (-3.14279680 * Math.Pow(10, (-5))) * Ta * Ta * D_Tmrt * Pa +
              (2.59835559 * Math.Pow(10, (-6))) * Ta * Ta * Ta * D_Tmrt * Pa +
              (-4.77136523 * Math.Pow(10, (-8))) * Ta * Ta * Ta * Ta * D_Tmrt * Pa +
              (8.64203390 * Math.Pow(10, (-3))) * va * D_Tmrt * Pa +
              (-6.87405181 * Math.Pow(10, (-4))) * Ta * va * D_Tmrt * Pa +
              (-9.13863872 * Math.Pow(10, (-6))) * Ta * Ta * va * D_Tmrt * Pa +
              (5.15916806 * Math.Pow(10, (-7))) * Ta * Ta * Ta * va * D_Tmrt * Pa +
              (-3.59217476 * Math.Pow(10, (-5))) * va * va * D_Tmrt * Pa +
              (3.28696511 * Math.Pow(10, (-5))) * Ta * va * va * D_Tmrt * Pa +
              (-7.10542454 * Math.Pow(10, (-7))) * Ta * Ta * va * va * D_Tmrt * Pa +
              (-1.24382300 * Math.Pow(10, (-5))) * va * va * va * D_Tmrt * Pa +
              (-7.38584400 * Math.Pow(10, (-9))) * Ta * va * va * va * D_Tmrt * Pa +
              (2.20609296 * Math.Pow(10, (-7))) * va * va * va * va * D_Tmrt * Pa +
              (-7.32469180 * Math.Pow(10, (-4))) * D_Tmrt * D_Tmrt * Pa +
              (-1.87381964 * Math.Pow(10, (-5))) * Ta * D_Tmrt * D_Tmrt * Pa +
              (4.80925239 * Math.Pow(10, (-6))) * Ta * Ta * D_Tmrt * D_Tmrt * Pa +
              (-8.75492040 * Math.Pow(10, (-8))) * Ta * Ta * Ta * D_Tmrt * D_Tmrt * Pa +
              (2.77862930 * Math.Pow(10, (-5))) * va * D_Tmrt * D_Tmrt * Pa +
              (-5.06004592 * Math.Pow(10, (-6))) * Ta * va * D_Tmrt * D_Tmrt * Pa +
              (1.14325367 * Math.Pow(10, (-7))) * Ta * Ta * va * D_Tmrt * D_Tmrt * Pa +
              (2.53016723 * Math.Pow(10, (-6))) * va * va * D_Tmrt * D_Tmrt * Pa +
              (-1.72857035 * Math.Pow(10, (-8))) * Ta * va * va * D_Tmrt * D_Tmrt * Pa +
              (-3.95079398 * Math.Pow(10, (-8))) * va * va * va * D_Tmrt * D_Tmrt * Pa +
              (-3.59413173 * Math.Pow(10, (-7))) * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (7.04388046 * Math.Pow(10, (-7))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (-1.89309167 * Math.Pow(10, (-8))) * Ta * Ta * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (-4.79768731 * Math.Pow(10, (-7))) * va * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (7.96079978 * Math.Pow(10, (-9))) * Ta * va * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (1.62897058 * Math.Pow(10, (-9))) * va * va * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (3.94367674 * Math.Pow(10, (-8))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (-1.18566247 * Math.Pow(10, (-9))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (3.34678041 * Math.Pow(10, (-10))) * va * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (-1.15606447 * Math.Pow(10, (-10))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * Pa +
              (-2.80626406) * Pa * Pa +
              (0.548712484) * Ta * Pa * Pa +
              (-0.00399428410) * Ta * Ta * Pa * Pa +
              (-9.54009191 * Math.Pow(10, (-4))) * Ta * Ta * Ta * Pa * Pa +
              (1.93090978 * Math.Pow(10, (-5))) * Ta * Ta * Ta * Ta * Pa * Pa +
              (-0.308806365) * va * Pa * Pa +
              (0.0116952364) * Ta * va * Pa * Pa +
              (4.95271903 * Math.Pow(10, (-4))) * Ta * Ta * va * Pa * Pa +
              (-1.90710882 * Math.Pow(10, (-5))) * Ta * Ta * Ta * va * Pa * Pa +
              (0.00210787756) * va * va * Pa * Pa +
              (-6.98445738 * Math.Pow(10, (-4))) * Ta * va * va * Pa * Pa +
              (2.30109073 * Math.Pow(10, (-5))) * Ta * Ta * va * va * Pa * Pa +
              (4.17856590 * Math.Pow(10, (-4))) * va * va * va * Pa * Pa +
              (-1.27043871 * Math.Pow(10, (-5))) * Ta * va * va * va * Pa * Pa +
              (-3.04620472 * Math.Pow(10, (-6))) * va * va * va * va * Pa * Pa +
              (0.0514507424) * D_Tmrt * Pa * Pa +
              (-0.00432510997) * Ta * D_Tmrt * Pa * Pa +
              (8.99281156 * Math.Pow(10, (-5))) * Ta * Ta * D_Tmrt * Pa * Pa +
              (-7.14663943 * Math.Pow(10, (-7))) * Ta * Ta * Ta * D_Tmrt * Pa * Pa +
              (-2.66016305 * Math.Pow(10, (-4))) * va * D_Tmrt * Pa * Pa +
              (2.63789586 * Math.Pow(10, (-4))) * Ta * va * D_Tmrt * Pa * Pa +
              (-7.01199003 * Math.Pow(10, (-6))) * Ta * Ta * va * D_Tmrt * Pa * Pa +
              (-1.06823306 * Math.Pow(10, (-4))) * va * va * D_Tmrt * Pa * Pa +
              (3.61341136 * Math.Pow(10, (-6))) * Ta * va * va * D_Tmrt * Pa * Pa +
              (2.29748967 * Math.Pow(10, (-7))) * va * va * va * D_Tmrt * Pa * Pa +
              (3.04788893 * Math.Pow(10, (-4))) * D_Tmrt * D_Tmrt * Pa * Pa +
              (-6.42070836 * Math.Pow(10, (-5))) * Ta * D_Tmrt * D_Tmrt * Pa * Pa +
              (1.16257971 * Math.Pow(10, (-6))) * Ta * Ta * D_Tmrt * D_Tmrt * Pa * Pa +
              (7.68023384 * Math.Pow(10, (-6))) * va * D_Tmrt * D_Tmrt * Pa * Pa +
              (-5.47446896 * Math.Pow(10, (-7))) * Ta * va * D_Tmrt * D_Tmrt * Pa * Pa +
              (-3.59937910 * Math.Pow(10, (-8))) * va * va * D_Tmrt * D_Tmrt * Pa * Pa +
              (-4.36497725 * Math.Pow(10, (-6))) * D_Tmrt * D_Tmrt * D_Tmrt * Pa * Pa +
              (1.68737969 * Math.Pow(10, (-7))) * Ta * D_Tmrt * D_Tmrt * D_Tmrt * Pa * Pa +
              (2.67489271 * Math.Pow(10, (-8))) * va * D_Tmrt * D_Tmrt * D_Tmrt * Pa * Pa +
              (3.23926897 * Math.Pow(10, (-9))) * D_Tmrt * D_Tmrt * D_Tmrt * D_Tmrt * Pa * Pa +
              (-0.0353874123) * Pa * Pa * Pa +
              (-0.221201190) * Ta * Pa * Pa * Pa +
              (0.0155126038) * Ta * Ta * Pa * Pa * Pa +
              (-2.63917279 * Math.Pow(10, (-4))) * Ta * Ta * Ta * Pa * Pa * Pa +
              (0.0453433455) * va * Pa * Pa * Pa +
              (-0.00432943862) * Ta * va * Pa * Pa * Pa +
              (1.45389826 * Math.Pow(10, (-4))) * Ta * Ta * va * Pa * Pa * Pa +
              (2.17508610 * Math.Pow(10, (-4))) * va * va * Pa * Pa * Pa +
              (-6.66724702 * Math.Pow(10, (-5))) * Ta * va * va * Pa * Pa * Pa +
              (3.33217140 * Math.Pow(10, (-5))) * va * va * va * Pa * Pa * Pa +
              (-0.00226921615) * D_Tmrt * Pa * Pa * Pa +
              (3.80261982 * Math.Pow(10, (-4))) * Ta * D_Tmrt * Pa * Pa * Pa +
              (-5.45314314 * Math.Pow(10, (-9))) * Ta * Ta * D_Tmrt * Pa * Pa * Pa +
              (-7.96355448 * Math.Pow(10, (-4))) * va * D_Tmrt * Pa * Pa * Pa +
              (2.53458034 * Math.Pow(10, (-5))) * Ta * va * D_Tmrt * Pa * Pa * Pa +
              (-6.31223658 * Math.Pow(10, (-6))) * va * va * D_Tmrt * Pa * Pa * Pa +
              (3.02122035 * Math.Pow(10, (-4))) * D_Tmrt * D_Tmrt * Pa * Pa * Pa +
              (-4.77403547 * Math.Pow(10, (-6))) * Ta * D_Tmrt * D_Tmrt * Pa * Pa * Pa +
              (1.73825715 * Math.Pow(10, (-6))) * va * D_Tmrt * D_Tmrt * Pa * Pa * Pa +
              (-4.09087898 * Math.Pow(10, (-7))) * D_Tmrt * D_Tmrt * D_Tmrt * Pa * Pa * Pa +
              (0.614155345) * Pa * Pa * Pa * Pa +
              (-0.0616755931) * Ta * Pa * Pa * Pa * Pa +
              (0.00133374846) * Ta * Ta * Pa * Pa * Pa * Pa +
              (0.00355375387) * va * Pa * Pa * Pa * Pa +
              (-5.13027851 * Math.Pow(10, (-4))) * Ta * va * Pa * Pa * Pa * Pa +
              (1.02449757 * Math.Pow(10, (-4))) * va * va * Pa * Pa * Pa * Pa +
              (-0.00148526421) * D_Tmrt * Pa * Pa * Pa * Pa +
              (-4.11469183 * Math.Pow(10, (-5))) * Ta * D_Tmrt * Pa * Pa * Pa * Pa +
              (-6.80434415 * Math.Pow(10, (-6))) * va * D_Tmrt * Pa * Pa * Pa * Pa +
              (-9.77675906 * Math.Pow(10, (-6))) * D_Tmrt * D_Tmrt * Pa * Pa * Pa * Pa +
              (0.0882773108) * Pa * Pa * Pa * Pa * Pa +
              (-0.00301859306) * Ta * Pa * Pa * Pa * Pa * Pa +
              (0.00104452989) * va * Pa * Pa * Pa * Pa * Pa +
              (2.47090539 * Math.Pow(10, (-4))) * D_Tmrt * Pa * Pa * Pa * Pa * Pa +
              (0.00148348065) * Pa * Pa * Pa * Pa * Pa * Pa;
            #endregion

            return UTCI_approx;
        }


        /// <summary>
        /// Calc saturation vapour pressure
        /// </summary>
        /// <param name="ta">Input air temperature, degC</param>
        /// <returns></returns>
        private static double es(double ta)
        {
            //calculates saturation vapour pressure over water in hPa for input air temperature (ta) in celsius according to:
            //Hardy, R.; ITS-90 Formulations for Vapor Pressure, Frostpoint Temperature, Dewpoint Temperature and Enhancement Factors in the Range -100 to 100 °C; 
            //Proceedings of Third International Symposium on Humidity and Moisture; edited by National Physical Laboratory (NPL), London, 1998, pp. 214-221
            //http://www.thunderscientific.com/tech_info/reflibrary/its90formulas.pdf (retrieved 2008-10-01)

            double[] g = new double[] { -2836.5744, -6028.076559, 19.54263612, -0.02737830188, 0.000016261698, ((double)(7.0229056 * Math.Pow(10, -10))), ((double)(-1.8680009 * Math.Pow(10, -13))) };
            double tk = ta + 273.15;
            double es = 2.7150305 * Math.Log(tk);
            //for count, i in enumerate(g):
            for (int count = 0; count < g.Length; count++)
            {
                double i = g[count];
                es = es + (i * Math.Pow(tk, (count - 2)));
            }
            es = Math.Exp(es) * 0.01;
            return es;
        }


        public static InputsChecks CheckIfInputsValid(double Ta, double va, double Tmrt, double hum)
        {

        if (Ta < -50.0 || Ta > 50.0) return InputsChecks.Temp_OutOfRange;
        if (Tmrt-Ta < -30.0 || Tmrt-Ta > 70.0) return InputsChecks.Large_Gap_Between_Trmt_Ta;
        if (va < 0.5) return InputsChecks.WindSpeed_Too_Low;
        if (va > 17) return InputsChecks.WindSpeed_TooHigh;
        return InputsChecks.Pass;
        }

        public enum InputsChecks { Temp_OutOfRange, Large_Gap_Between_Trmt_Ta, WindSpeed_Too_Low, WindSpeed_TooHigh, Pass, Unknown }
       

    }

References

Papers presenting the UTCI:

  • UTCI poster, 13th International Conference on Environmental Ergonomics, Boston, Massachusetts, USA, 2-7 Aug 2009

Papers utilising the UTCI:

  • Journal article Sookuk Park, Stanton E. Tuller, Myunghee Jo, Application of Universal Thermal Climate Index (UTCI) for microclimatic analysis in urban thermal environments, Landscape and Urban Planning, Volume 125, May 2014, Pages 146-155
  • Journal article Katerina Pantavou, George Theoharatos, Mattheos Santamouris, Dimosthenis Asimakopoulos, Outdoor thermal sensation of pedestrians in a Mediterranean climate and a comparison with UTCI, Building and Environment, Volume 66, August 2013, Pages 82-95, ISSN 0360-1323, http://dx.doi.org/10.1016/j.buildenv.2013.02.014.

Area of a triangle in 3D: C# code

The area of a triangle in 3D space can easily be calculated using Heron’s Formula.

The C# code below contains a method that returns the area of a triangle formed by 3 points. This code is written for RhinoCommon, though can be easily adapted for any C# application. ‘Point3d’ is a collection of XYZ coordinates for a single point, and the DistanceTo method returns a double equivalent to the Euclidean distance between the two points.

  public double AreaOfTriangle(Point3d pt1, Point3d pt2, Point3d pt3)
  {
    double a = pt1.DistanceTo(pt2);
    double b = pt2.DistanceTo(pt3);
    double c = pt3.DistanceTo(pt1);
    double s = (a + b + c) / 2;
    return Math.Sqrt(s * (s-a) * (s-b) * (s-c));
  }

References

Triangulate a quad mesh in C#

How to take a mesh of quad faces and return a mesh with triangle faces.

The principle of the algorithm is to look at each quad and split them into two triangles. It chooses the split by the shortest diagonal across the quad.

The code is written in C# for Rhino/Grasshopper, using the Rhino mesh structure. However, it can be easily adapted to any mesh application.

  public Mesh Triangulate(Mesh x)
  {
    int facecount = x.Faces.Count;
    for (int i = 0; i < facecount; i++)
    {
      var mf = x.Faces[i];
      if(mf.IsQuad)
      {
        double dist1 = x.Vertices[mf.A].DistanceTo(x.Vertices[mf.C]);
        double dist2 = x.Vertices[mf.B].DistanceTo(x.Vertices[mf.D]);
        if (dist1 > dist2)
        {
          x.Faces.AddFace(mf.A, mf.B, mf.D);
          x.Faces.AddFace(mf.B, mf.C, mf.D);
        }
        else
        {
          x.Faces.AddFace(mf.A, mf.B, mf.C);
          x.Faces.AddFace(mf.A, mf.C, mf.D);
        }
      }
    }

    var newfaces = new List<MeshFace>();
    foreach (var mf in x.Faces)
    {
      if(mf.IsTriangle) newfaces.Add(mf);
    }

    x.Faces.Clear();
    x.Faces.AddFaces(newfaces);
    return x;
  }

Before and after:

triangulate mesh

Make buildings with heights in Elk for Grasshopper

I have recently been constructing whole cities in Rhino using the Elk plugin. This parses OpenStreetMap data into Grasshopper geometry, allowing you to visualise any city or area in the world in your Rhino viewport.

York in Grasshopper with Elk OpenStreetMap data

One of the most interesting ways of getting your cities to look like cities is getting the buildings right. It is possible to extract building data with Elk, but this isn’t intuitive if you aren’t already familiar with OpenStreetMap data. And even if you are, the output is a collection of points, which requires further work to turn it into actual buildings.

This article will show you how I created buildings by extracting the OSM data and converting them into 3D meshes.

OpenStreetMap: Understanding the data

A crash course into OpenStreetMap data: All (well, nearly all) objects in the map are either saved as points or as lists of points. Points are useful for small objects, such as benches, letterboxes or trees. For larger objects, such as roads and buildings, collections of points are used. For roads, these points join together to form lines along the centre of the road. For buildings, these points define the line around the building’s edge. These ‘point collections’ are essentially polylines.

Every object, whether a point or a polyline, has a list of data associated with it. Each item in this list has a key and a value. It is with these keys and values that we describe the object. The most common key is ‘name’, and we describe the name in the value field. Most objects have many tags. For example, if we go into the OpenStreetMap editor and have a look at a local branch of Costa Coffee:

OpenStreetMap tags values keys example

We have a list of keys and a list of values. The values are the data itself; the keys describe the type of data.

If you want to see this for yourself, go into the editor on OpenStreetMap. I personally prefer the Potlatch2 editor, which you can find in the drop-down next to the ‘edit’ button at the top. To see the tags, select an object on the map, then click ‘advanced’ in the bottom left.

Buildings in OpenStreetMap

Similarly, all buildings contain a collection of tags. The great thing about tags is that they are an open concept – you can use any tags that you like. With buildings, the most common tags include the building name and the building type. For example:

OpenStreetMap tags values keys example building

Using Elk to extract buildings

Elk can be used to extract the points that form the building outline. Like polylines in Rhino, the data is saved as a collection of points, and not a line itself, so it will be up to us to stitch the points together to create a building outline.

There is no built-in component that returns directly the building points, but we can use the GenericOSM to filter for data containing the ‘building’ key. The Polyline component joins the points together.

Grasshopper components Elk extract buildings

building outlines openstreetmap elk grasshopper

Make your buildings 3D

This is all well and good, but don’t they look a bit flat and boring? Let’s make them look a bit more realistic.

The easiest way to turn your polylines into 3D buildings is to extrude them, and then use patch to create a roof. But I can tell you through my own experience that this is a bad idea. For a few buildings it’s okay, but for the city scale, working with surfaces is very slow and you’ll quickly see your computer grind to a halt. To build our buildings at lightning speed, we have to use meshes.

There isn’t anything natively in Grasshopper that does this for us, but we can quickly write something in C#. Basically, we build up the walls with mesh faces, then use a Rhino command to cap the top for the roof.

This script takes in a list of points that describe the building outline, and a value for its height. (Let’s just send it a value of 10m or so for now.)

  private void RunScript(List<Point3d> pts, double ht, ref object A)
  {

    var building = new Mesh();

    //make walls
    for (int p = 0; p < pts.Count; p++)
    {
      building.Vertices.Add(pts[p]);
      building.Vertices.Add(new Point3d(pts[p].X, pts[p].Y, pts[p].Z + ht));
    }

    for (int p = 0; p < pts.Count - 1; p++)
    {
      int j = p * 2;
      building.Faces.AddFace(j, j + 1, j + 3, j + 2);
    }

    //make roof
    var roofpts = new List<Point3d>();
    for (int p = 0; p < pts.Count; p++)
    {
      roofpts.Add(building.Vertices[p * 2 + 1]);
    }
    var pline = new Polyline(roofpts);
    var roof = Mesh.CreateFromClosedPolyline(pline);
    building.Append(roof);

    A = building;

  }

This then gives us:

Elk Grasshopper example buildings

Elk Grasshopper example buildings

But not all buildings are 10 metres tall…

It made things a lot easier to assume a height for our buildings. But can we do any better?

Given that we have a height input, we should be able to put something a bit more sensible into it. Some buildings in OSM do come with height data, though most don’t. If they do, this information is under the height key. How can we extract the building’s height information and apply it to our buildings with Elk?

It currently isn’t easy as there isn’t a comprehensive tag filter within Elk. One solution is to use the GenericOSM with k=height. This will return everything with height data; we just have to assume that everything returned is a building (it usually is) and model it as such.

Set up your Grasshopper as below, using the same C# script as above to create the buildings:

Elk Grasshopper example buildings

For my example of York, barely a single building has any height data. But, very happily, one very patient mapper has recorded the height of all the different elements of York Minster, leading to a very pleasing model.

But I really want heights on ALL my buildings!

Then you’ll likely have to pay up.

At least in the UK, the only near-comprehensive source of building heights is via the Ordnance Survey Topography Layer. Limited amounts of data are available as free academic licences, but otherwise it ain’t cheap.

In the meantime, if you’ve made it this far, you’ve probably realised that there are a lot of gaps in the OSM database. These gaps are best filled by people with local knowledge where you live, so I would encourage you to register and to start mapping! 🙂

Orient a Grasshopper mesh so that its normals face upwards

How to read the normal of a mesh in Grasshopper in C#, and flip the mesh if the normals are facing the wrong way.

Creating city buildings in Rhino

I recently revisited the task of generating cities in Rhino using Elk. One of the problems with this original solution was that I had no fast way of generating the roofs of the buildings. The most obvious solution to generate the building roofs was to use the ‘patch’ function of Rhino using the building outline as input. But surfaces are data- and processor-heavy, and files at the city scale would crash the computer. So I left the roofs out…

Rendering Park Street in Bristol in Grasshopper and Rhino using the Elk plugin and OpenStreetMap data.

Meshes are much lighter data structures than surfaces, and should be used where possible where performance is an issue. In this post, meshes were created by casting curves to meshes.

Mesh orientation

This works well, but the output meshes do have rendering issues. All mesh faces have a direction (a front and a back) and Rhino renders the mesh differently depending on what side it thinks it’s looking at. It is apparently quite random whether the above meshing trick generates a mesh which faces upwards or downwards.

Grasshopper mesh vector orientation problem on buildings

Flip backwards meshes

The solution is to ‘flip’ the offending meshes so that all meshes are facing the same way. The challenge lies in detecting the meshes which are facing the wrong way, and then to find a way to flip these meshes. The tidiest way is to do this with a C# component.

  private void RunScript(object x, object y, ref object A)
  {

    Mesh mesh = (Mesh) x;
    for(int i = 0; i < mesh.Faces.Count; i++)
    {
      var normal = mesh.Normals[0];
      if(normal.Z < 0)
      {
        mesh.Flip(true, true, true);
      }
    }

    A = mesh;

  }

The result is that the roofs now are all the same colour. The red lines, representing the normals of the mesh faces, are all now facing the same direction.

Grasshopper vectors on mesh direction problem

Run a Grasshopper component from within your C# code

How to call and calculate a Grasshopper component from within some C# code, and read and return the component outputs.

A Grasshopper component is essentially a visual interpretation of a method in programming. It has inputs, it does calculations, and it produces outputs. Grasshopper components are also saved within DLL libraries, and can be referenced. So, surely, it’s possible to access a component programatically from within something like a Visual Studio project? This is a quick first attempt to do so.

The code below attempts to read one of my own components (“CalcSunDirection”). The component runs with all inputs at default values, and then returns the first data item within output 2 (the third one in human-speak). This is copy-pasted from the Solve_Instance method when creating Grasshopper components in Visual Studio.

        protected override void SolveInstance(IGH_DataAccess DA)
        {
            //Create the component and run calculations
            var cs = new MyComponents.Components.CalcSunDirection();
            cs.CreateAttributes();
            cs.ExpireSolution(true);

            //add to document
            GH_Document GrasshopperDocument = this.OnPingDocument();
            GrasshopperDocument.AddObject(cs, false);

            //read output[2]
            cs.Params.Output[2].CollectData();
            var rtnval = cs.Params.Output[2].VolatileData.get_Branch(0)[0];

            //remove that component
            GrasshopperDocument.RemoveObject(cs.Attributes, false);

            //send output
            DA.SetData(0, rtnval);
        }

Grasshopper component for calculating sun direction written in C#, being called from a second test component

As we can see, the test component produces the same output as the CalcSunDirection component it is referencing. The above image is for comparison – in reality, the user wouldn’t see the CalcSunDirection, only the Test component.

I believe it is hypothetically possible to do this trick with any component, assuming that the DLL/GHA file containing the component you want to use is referenced in your Visual Studio project.

I tried to do this with some native Grasshopper components (such as the circle from CNR component). I looked up the namespace of the component using this tool, but I had trouble locating the DLL containing the component, so I was unable to add it to my VS project. (For example, the Circle CNR component has namespace CurveComponents.Component_CircleCNR, which is not within Grasshopper.dll. Anyone have any idea where I can find it?) Edit – found them! See below…

As a first attempt, the code above also seems inefficient in that you have to physically add the component before the outputs become readable. I get around this from a user experience point of view by removing that component after, but computationally, it still feels heavy and unnecessary.

Upon reflection, what I’ve essentially created is a programmatic version of the clustering feature of Grasshopper. Is this the best way to go about it? If you have any interesting suggestions, please let me know 🙂

Update – geometry GHA files

Many thanks to Andrew Heumann for answering my question above – many of the components are not contained within Grasshopper.dll but are saved elsewhere.

It appears that since version 0.8.0012 or so, they have been kept buried within the Program Files. On various computers, I’ve found them at:

C:\Program Files\Common Files\McNeel\Rhinoceros\5.0\Plug-ins\Grasshopper\0.9.76.0\Components


C:\Users\jrams\AppData\Roaming\McNeel\Rhinoceros\5.0\Plug-ins\Grasshopper\0.9.76.0\Components

If you are struggling to find them, and you don’t mind giving third party software direct access to your computer’s Master File Table (!), then UltraSearch is the fastest way to find the GHA files.

Within this folder is a collection of GHA files (which is essentially a DLL with the extension changed).

The full list is:

  • Curve.gha
  • Field.gha
  • Galapagos.dll
  • GalapagosLibrary.gha
  • IOLibrary.gha
  • LegacyScript.gha
  • Mathematics.gha
  • Script.gha
  • Surface.gha
  • Transform.gha
  • Triangulation.gha
  • Vector.gha

Grasshopper GHA extension files

So for the Circle CNR component, I would find it by referencing the Curve.gha file.

Update 2

See this post for updated code. This updated code allows you to create a dummy document, so you don’t need to paste components on the live document.

Convert a Brep to a Mesh in Rhino/Grasshopper C#

How to convert a Rhino Brep to a Rhino Mesh using RhinoCommon. This method is suitable for use in Grasshopper development and the Grasshopper C# component.

Create meshes from Brep

The code below produces a list of customised meshes based upon an input Brep and some mesh settings. The examples are written as static extension classes for compiled components (so you can access it directly as a Brep method), though can be easily adapted for the C# component too.

        public static List<Mesh> BrepToMeshes(this Brep brep, double maxEdge)
        {
            Mesh[] mesh;
            MeshingParameters mp = new MeshingParameters();
            mp.MaximumEdgeLength = maxEdge;
            mesh = Mesh.CreateFromBrep(brep, mp);
            return mesh.ToList<Mesh>();
        }

This method essentially replicates the Grasshopper components below:

Grasshopper component mesh to Brep

The MeshingParameters class replicates the ‘Mesh Settings’ component. You can assign settings to your mesh by creating an instance of MeshingParameters and accessing its properties, much as I have done with MaximumEdgeLength.

Joining the meshes

The output is a list of meshes. If you want to truly replicate the Mesh Brep component, you will also need to join all meshes in the list into a single mesh. This can be done with the Append method:

        public static Mesh JoinMeshes(this List<Mesh> meshes)
        {
            var rtnmesh = new Mesh();
            foreach (Mesh mesh in meshes)
            {
                rtnmesh.Append(mesh);
            }
            return rtnmesh;
        }

And for completeness, you can call the methods in a single line:

        public static Mesh BrepToMesh(this Brep brep, double maxEdge)
        {
            return JoinMeshes(BrepToMeshes(brep, maxEdge));
        }

Create 2D Delaunay triangulation mesh with C# in Grasshopper

How to perform a Delaunay triangulation on a list of points mapped in 2D, using the C# component in Grasshopper.

Delaunay triangulation is a highly efficient algorithm which creates a triangulated mesh from a collection of points. This page shows how to create a 2D mesh from a collection of points on the XY plane.

Input

A list of Point3d. These points should already be mapped onto a 2D plane – ideally onto the XY plane.

Points Grasshopper for Delaunay triangulation

If your points aren’t mapped onto a 2D plane, you’ll need to do this in advance. The reason for this is that the Delaunay triangulation algorithm below uses the Node2 type – essentially like a point, but only with X and Y coordinates – since this algorithm produces a 2D mesh.

Output

A regular, Grasshopper-friendly mesh.

Delaunay mesh in Grasshopper with C#

Steps

  1. Convert Point3d into Node2
  2. Add Node2 to Node2List (that’s a list of Node2s, not “node-to-list”!)
  3. Calculate connectivity of mesh faces
  4. Construct and return mesh

C# code

The code below uses Grasshopper.dll to perform the Delaunay triangulation.

    //input
    List<Point3d> pts;

    //convert point3d to node2
    //grasshopper requres that nodes are saved within a Node2List for Delaunay
    var nodes = new Grasshopper.Kernel.Geometry.Node2List();
    for (int i = 0; i < pts.Count; i++)
    {
      //notice how we only read in the X and Y coordinates
      //  this is why points should be mapped onto the XY plane
      nodes.Append(new Grasshopper.Kernel.Geometry.Node2(pts[i].X, pts[i].Y));
    }

    //solve Delaunay
    var delMesh = new Mesh();
    var faces = new List<Grasshopper.Kernel.Geometry.Delaunay.Face>();
    
    faces = Grasshopper.Kernel.Geometry.Delaunay.Solver.Solve_Faces(nodes, 1);
    
    //output
    delMesh = Grasshopper.Kernel.Geometry.Delaunay.Solver.Solve_Mesh(nodes, 1, ref faces);

What next?

Delaunay meshes are pretty amazing. They are quick to generate, quick to analyse and quick to render. They generate sensible triangulation and require no more information than the input points. Unless you absolutely must have smooth surfaces and edges, don’t use a surface, use a mesh.

This video uses Delaunay triangulation to power the graph in the bottom left. The graph was easily coloured by associating each node in the mesh with a value.

These posts will help you get started in making the most of your mesh:

References